1. 최단 경로 알고리즘
- 목적지에 이르는 모든 가능한 경로 중 최단 경로를 찾는 알고리즘
- 종류: ①다익스트라 알고리즘 ②벨만-포드 알고리즘 ③모든 쌍 최단 경로 알고리즘
※ ①② 와 ③의 코딩테스트 제출 차이
- 특정 시작점에서 모든 정점들까지의 최단 경로 구하기
--> 다익스트라, 벨만-포드
- 모든 시작점에서 모든 정점들까지의 최단 경로 구하기
--> 모든 쌍 최단 경로 알고리즘 (대표: 플로이드와샬)
※ 최소 신장 VS 최단 경로
"최소 신장"과 "최단 경로"는 얼핏보면 같은 말 같다. 뭐가 다르길래 굳이 알고리즘을 나누었나 궁금하여 차이점을 간단히 메모해둔다.
* 최소 신장
- 모든 정점을 방문하면서 간선의 비용이 합이 최소가 되는 "트리"를 만듦
- ex) 프림 알고리즘, 크루스칼 알고리즘
* 최단 경로
- 무향 그래프 뿐만 아니라 유향 그래프도 가능
- 음의 가중치도 가능
- 출발지와 도착지가 존재 ("경로" 이므로)
2. 다익스트라 알고리즘(Dijkstra)
- 입력 그래프 G=(V,E)에서 간선들의 가중치가 모두 0이상일 때의 최단 경로 알고리즘.
- 가중치가 음이 되면 작동하지 않는다.
- 다익스트라가 고안
- 최소 신장 트리의 프림 알고리즘과 거의 유사
▶ 동작 예시
(a) 출발지를 A로 고정. A의 최단 경로만 0으로 표시. 나머지 정점들은 모두 ∞로 표시. 집합 S에 A를 포함한다.
S = {A}
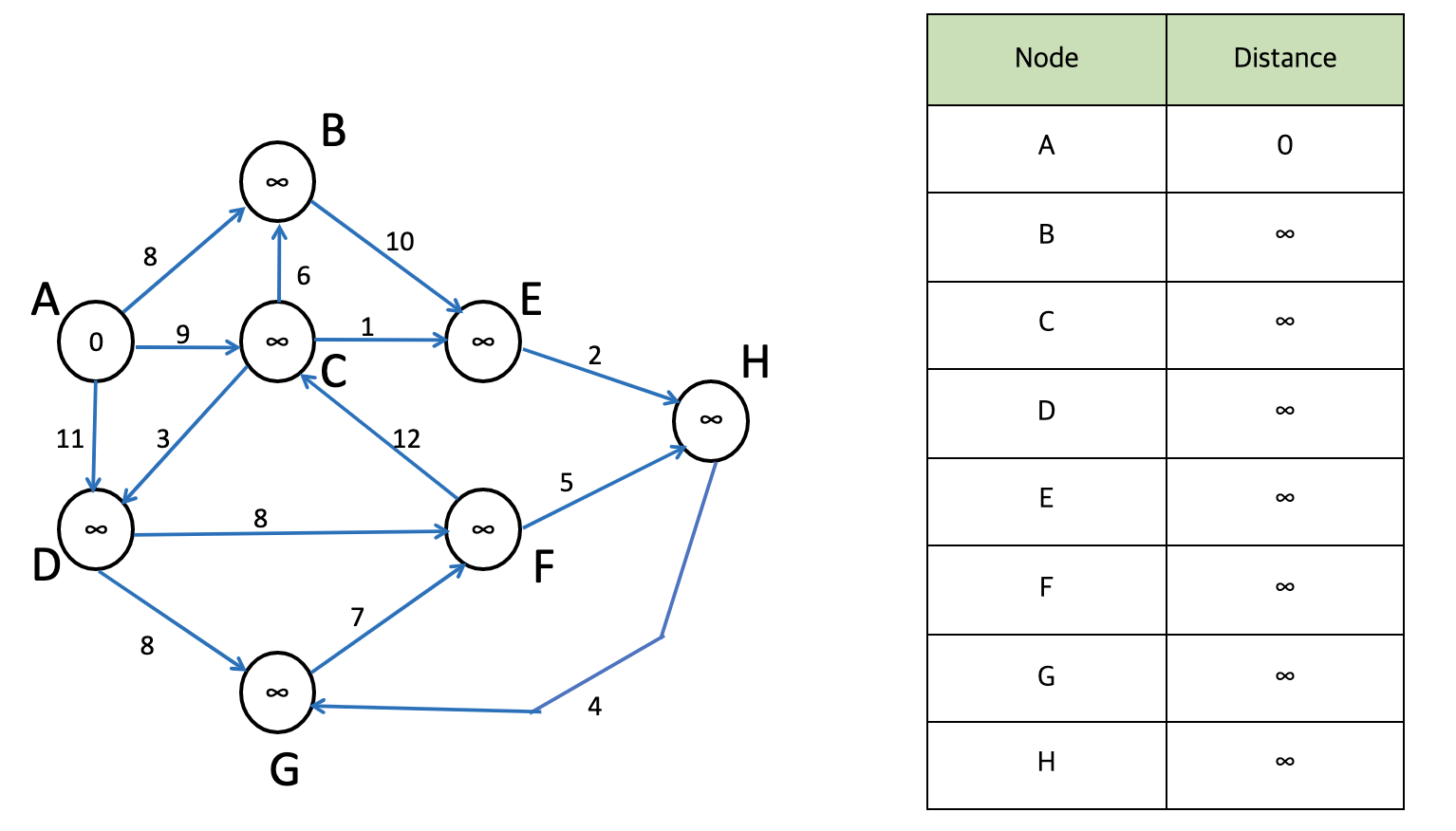
(b) 집합 S의 원소인 정점 A와 연결된 정점들까지의 간선 가중치를 살핀다. B(8), C(9), D(11)중 가장 최단 경로인 정점 B를 집합 S에 포함시킨다. (B,C,D 중 B를 고르는 방법은 min heap이용. heapify)
S = {A, B}

(c) 집합 S = {A, B}와 연결된 정점들의 가중치를 살핀다. C(9), D(11), E(18) 중 C가 가장 최단 경로이므로 집합 S에 C를 포함시킨다.
S = {A, B, C}

(d) 집합 S = {A, B, C}와 연결된 간선들의 가중치를 살핀다. D(11), E(10)중에 가장 최단 경로인 E를 집합 S에 포함시킨다.
S = {A, B, C, E}
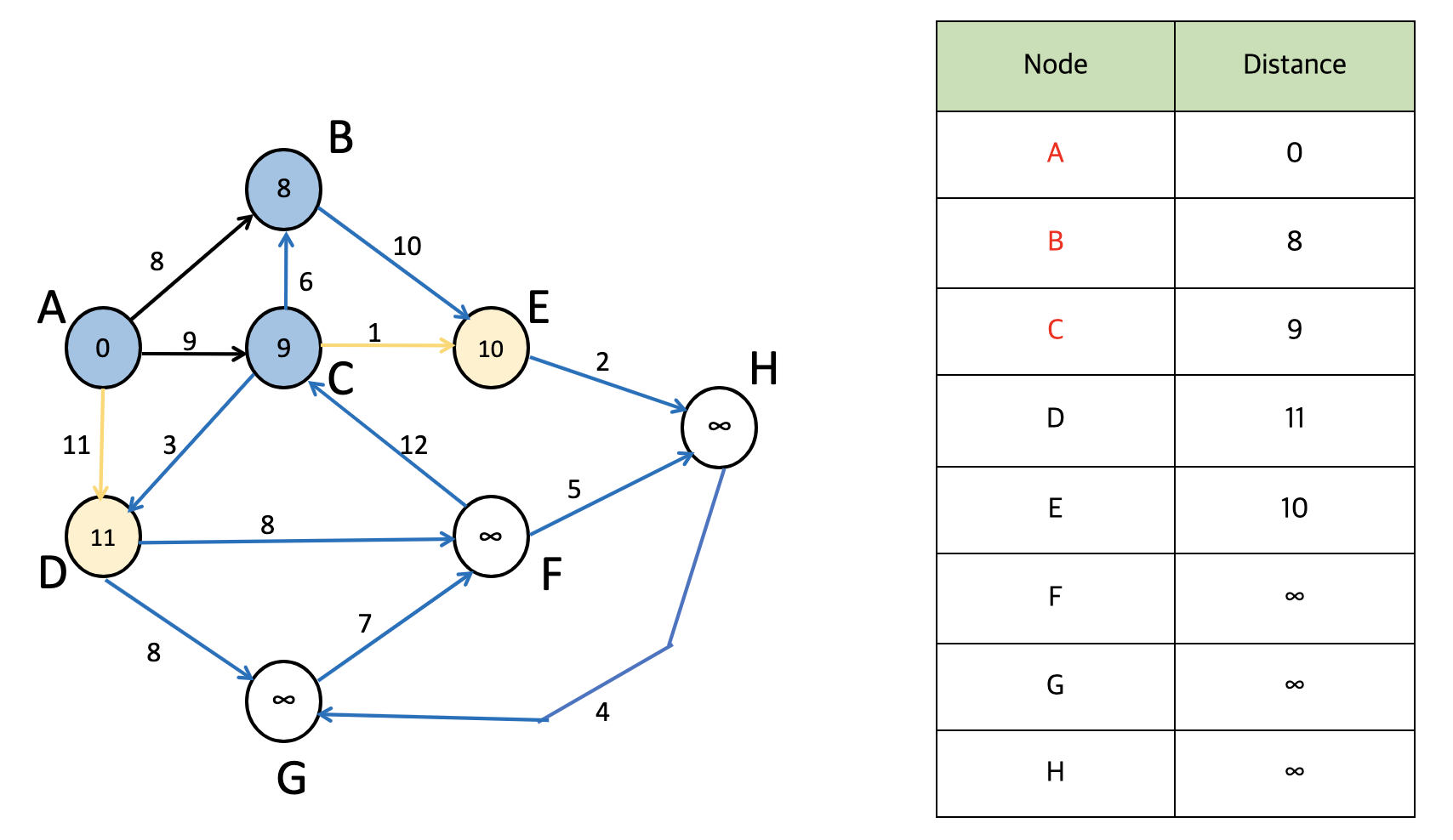
(e) 집합 S = {A, B, C, E}에 연결된 간선들의 가중치를 살핀다. D(11), H(12)중 최단 경로인 D를 집합 S에 포함시킨다.
S = {A, B, C, E, D}

(f) S = {A, B, C, E, D}에 연결된 간선들의 가중치를 살핀다. H(12), F(19), G(19)중 최단 경로인 H를 집합 S에 포함시킨다.
S = {A, B, C, E, D, H}

(g) S = {A, B, C, E, D, H}에 연결된 간선들의 가중치를 살핀다. F(19), G(16)중 최단 경로인 G를 집합 S에 포함시킨다.
S = {A, B, C, E, D, H, G}

(H) S = {A, B, C, E, D, H, G}에 연결된 간선들의 가중치를 살핀다. 마지막 간선인 F(19)를 집합 S에 포함시킨다.
S = {A, B, C, E, D, H, G,F}

(최종)

▶ 다익스트라 알고리즘이 동작하지 않는 경우
앞의 그래프에서 간선 하나를 음의 가중치로 바꿔 놓았다. 이 경우에 처음에는 A -> B까지의 최단 경로는 8이다. 그 다음에는 A -> C -> B를 통해 -6으로 바뀔 것이다. 하지만 다익스트라는 다음과 같은 규칙이 있다.
"집합 S에 포함된 정점에서는 최단거리를 다시 계산하지 않는다."
해당 규칙을 위반하므로 음의 가중치가 있는 그래프에서는 다익스트라 알고리즘이 작동하지 않는다.

3. 소스코드(JAVA)
package com.algorithm.thisiscodingtest.dijkstra;
import java.io.IOException;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.PriorityQueue;
public class Dijkstra {
static class Edge implements Comparable<Edge> {
int destination; // 도착지
int weight; // 가중치
Edge(int destination, int weight) {
this.destination = destination;
this.weight = weight;
}
@Override
public int compareTo(Edge o) {
return Integer.compare(this.weight, o.weight);
}
}
public static ArrayList<Edge> edges[];
public static boolean[] check;
public static int[] dist;
public static void main(String[] args) throws IOException {
int V = 8; // 정점 개수
int E = 14; // 간선 개수
int start = 1; // 출발지
edges = new ArrayList[V + 1];
for (int i = 1; i <= 8; i++) {
edges[i] = new ArrayList<>();
}
// 그래프 생성
// A:1, B:2, C:3, D:4, E:5, F:6, G:7, H:8
edges[1].add(new Edge(2, 8)); // A -8-> B
edges[1].add(new Edge(3, 9)); // A -9-> C
edges[1].add(new Edge(4, 11)); // A -11-> D
edges[2].add(new Edge(5, 10));// B -10-> E
edges[3].add(new Edge(2, 6));// C -6-> B
edges[3].add(new Edge(5, 1));// C -1-> E
edges[3].add(new Edge(4, 3));// C -3-> D
edges[4].add(new Edge(6, 8));// D -8-> F
edges[4].add(new Edge(7, 8));// D -8-> G
edges[5].add(new Edge(8, 2));// E -2-> H
edges[6].add(new Edge(3, 12));// F -12-> C
edges[6].add(new Edge(8, 5));// F -5-> H
edges[7].add(new Edge(6, 7));// G -7-> F
edges[8].add(new Edge(7, 4)); // H -4-> G
check = new boolean[V + 1];
dist = new int[V + 1];
dijkstra(start);
String[] strings = {"", "A", "B", "C", "D", "E", "F", "G", "H"};
for (int i = 1; i <= 8; i++) {
System.out.println(strings[i] + " = " + dist[i]);
}
}
public static void dijkstra(int start) {
PriorityQueue<Edge> pq = new PriorityQueue<>();
Arrays.fill(dist, Integer.MAX_VALUE);
pq.add(new Edge(start, 0));
dist[start] = 0;
while (!pq.isEmpty()) {
Edge edge = pq.poll();
int destination = edge.destination;
if (check[destination]) {
continue;
} else {
check[destination] = true;
}
for (Edge next : edges[destination]) {
if (dist[next.destination] >= dist[destination] + next.weight) {
dist[next.destination] = dist[destination] + next.weight;
pq.add(new Edge(next.destination, dist[next.destination]));
}
}
}
}
}[출력]
A = 0
B = 8
C = 9
D = 11
E = 10
F = 19
G = 16
H = 12
Process finished with exit code 0
'알고리즘' 카테고리의 다른 글
| [Java] 에라토스테네스의 체 - 소수 판별 (0) | 2021.04.07 |
|---|---|
| 이분 탐색(Binary Search) (0) | 2021.01.27 |
| LRU(Least Recently Used) 캐시 알고리즘 (0) | 2020.11.14 |
